Figuring out Numbers
So I was having a play, again, this time with a further look into composites and primes.I am curious to play with representations of digits in manners that allow visualization of distributions of prime numbers and non-prime numbers... not naively in any form or shape of faith in finding something someone else hasn't of course, just because it's fun, for me, to look, play, learn and figure things out by myself...
So what did I get to - from this point on, it may well seem absolutely obvious, already known/common fact - but this is playful musings, explored with no math guides or prior knowledge applied, this is number theory basics a la Chris.
'Types' of Numbers...
My number playing revolves around positive integers... of which a number is categorized in this exercise, as composite or prime.
With this, a couple of terms are thrown around which you may be familiar with:
With this, a couple of terms are thrown around which you may be familiar with:
Factor
The complete list of factors of 52 is: 1, 2, 4, 13, 26, and 52 (all these divide exactly into 52).
Prime Number
A prime number is a whole number greater than 1, whose only two whole-number factors are 1 and itself.
I particularly liked this visual example of what a prime number is:
Composite Number
Sourcing, Manipulation, Confirmation!
Manually formulating a table for all factors of a number seemed like an unnecessary task to proceed with, seeing as what I wanted to delve into being already somewhat of a large task.
So I scoured the net for a table as such, and this is what I found.
Which for a quick display of the content, it looks something like this:
- d(n) is the number of positive divisors of n, including 1 and n itself
- σ(n) is the sum of all the positive divisors of n, including 1 and n itself
- s(n) is the sum of the proper divisors of n, which does not include n itself; that is, s(n) = σ(n) − n
- a perfect number equals the sum of its proper divisors; that is, s(n) = n
- a deficient number is greater than the sum of its proper divisors; that is, s(n) < n
- an abundant number is less than the sum of its proper divisors; that is, s(n) > n
- a prime number has only 1 and itself as divisors; that is, d(n) = 2. Prime numbers are always deficient as s(n)=1
Taking this data and loading it into Excel, allows me to manipulate and produce variations in data representation for the fun of spotting characteristics, similarities/groupings and/or patterns... but what it did lead to, actually saw me producing the results manually with the application of formula in Excel - so in fact, the table, in the end, was just a confirmation base for my calculations and output.
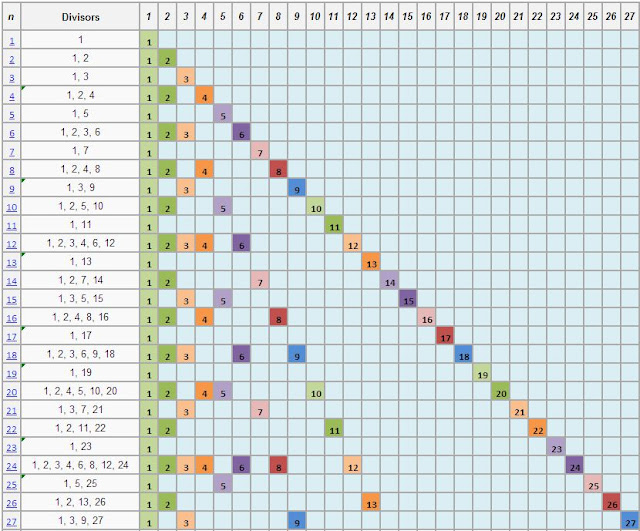
The below shows the divisors for n from the source table; to the right, in the grid and with colors - is the output of a formula, that divides n by all whole integers presented in the top row increasing by 1 across column by column - but only is the product of the division displayed, if the value is a whole integer.
The diagonal line is the boundary of this output as that is the indicator of where n is divided by n.
Any whole integer in that top row, as a divisor of n, will not be whole if it is >n, and so, will not display a populated number.
Any whole integer in that top row, as a divisor of n, will not be whole if it is >n, and so, will not display a populated number.
The results of this simple formula, produce the same outputs as what I found on on Wikipedia - allowing me to produce my own counts and sums of divisors of positive whole integers and therefore adding additional columns to flag whether n is prime or not! (Prime is identified in this grid, as n where the count of divisors = 2 & the sum of divisors = n + 1)
The coloring may already present some structural reference to the distribution of numbers as divisors of n.
A Stopping Point... for now...
There is more I would like to output on this what I have started to clean up from previous weeks play - however, as per usual, I digressed... and what I produced just now will form a separate post for reference, as I have branched back into an area I already have some background work on, but tidied a portion up for its potential supporting role in analysis of tentative primes...
Which is to say, the above work leads on to flagging of numbers, based on criteria such as last digit and then mod9 and square root check - to identify definite NON PRIMES; and potential primes... which I had a little curiosity to check whether permutations of base numbers (i.e. 123, 132, 213, 231, 312, 321) can occur where all permutations are prime; whether there is some significance of digit positioning with regards to permutations and prime elements and so on...
It got to well past 4am so... I want to wrap this part up and come back to it, as this what I posted today, is just the tip of the iceberg of what outputs I would like to share! That's just the way such analysis seems to go, from A to B to C through to Z and then sometimes coming back to A :D